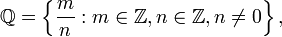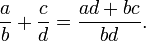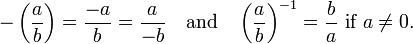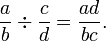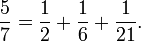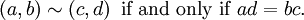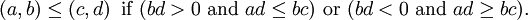Rational number
Background Information
SOS Children, which runs nearly 200 sos schools in the developing world, organised this selection. Visit the SOS Children website at http://www.soschildren.org/
In mathematics, a rational number is a number which can be expressed as a ratio of two integers. Non-integer rational numbers (commonly called fractions) are usually written as the vulgar fraction 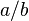 , where b is not zero. a is called the numerator, and b the denominator.
, where b is not zero. a is called the numerator, and b the denominator.
Each rational number can be written in infinitely many forms, such as  , but it is said to be in simplest form when a and b have no common divisors except 1 (i.e., they are coprime). Every non-zero rational number has exactly one simplest form of this type with a positive denominator. A fraction in this simplest form is said to be an irreducible fraction, or a fraction in reduced form.
, but it is said to be in simplest form when a and b have no common divisors except 1 (i.e., they are coprime). Every non-zero rational number has exactly one simplest form of this type with a positive denominator. A fraction in this simplest form is said to be an irreducible fraction, or a fraction in reduced form.
The decimal expansion of a rational number is eventually periodic (in the case of a finite expansion the zeroes which implicitly follow it form the periodic part). The same is true for any other integral base above one, and is also true when rational numbers are considered to be p-adic numbers rather than real numbers. Conversely, if the expansion of a number for one base is periodic, it is periodic for all bases and the number is rational. A real number that is not a rational number is called an irrational number.
The set of all rational numbers, which constitutes a field, is denoted  . Using the set-builder notation,
. Using the set-builder notation,  is defined as
is defined as
where 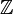 denotes the set of integers.
denotes the set of integers.
The term rational
In the mathematical world, the adjective rational often means that the underlying field considered is the field  of rational numbers. For example, a rational integer is an algebraic integer which is also a rational number, which is to say, an ordinary integer, and a rational matrix is a matrix whose coefficients are rational numbers. Rational polynomial usually, and most correctly, means a polynomial with rational coefficients, also called a “polynomial over the rationals”. However, rational function does not mean the underlying field is the rational numbers, and a rational algebraic curve is not an algebraic curve with rational coefficients.
of rational numbers. For example, a rational integer is an algebraic integer which is also a rational number, which is to say, an ordinary integer, and a rational matrix is a matrix whose coefficients are rational numbers. Rational polynomial usually, and most correctly, means a polynomial with rational coefficients, also called a “polynomial over the rationals”. However, rational function does not mean the underlying field is the rational numbers, and a rational algebraic curve is not an algebraic curve with rational coefficients.
Arithmetic
Two rational numbers 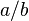 and
and 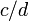 are equal if and only if
are equal if and only if  .
.
Two fractions are added as follows
The rule for multiplication is
Additive and multiplicative inverses exist in the rational numbers
It follows that the quotient of two fractions is given by
Egyptian fractions
Any positive rational number can be expressed as a sum of distinct reciprocals of positive integers, such as
For any positive rational number, there are infinitely many different such representations, called Egyptian fractions, as they were used by the ancient Egyptians. The Egyptians also had a different notation for dyadic fractions.
Formal construction
Mathematically we may construct the rational numbers as equivalence classes of ordered pairs of integers  , with
, with 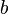 not equal to zero. We can define addition and multiplication of these pairs with the following rules:
not equal to zero. We can define addition and multiplication of these pairs with the following rules:
and if c ≠ 0, division by
The intuition is that  stands for the number denoted by the fraction
stands for the number denoted by the fraction  To conform to our expectation that
To conform to our expectation that 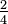 and
and  denote the same number, we define an equivalence relation
denote the same number, we define an equivalence relation  on these pairs with the following rule:
on these pairs with the following rule:
This equivalence relation is a congruence relation: it is compatible with the addition and multiplication defined above, and we may define Q to be the quotient set of ~, i.e. we identify two pairs (a, b) and (c, d) if they are equivalent in the above sense. (This construction can be carried out in any integral domain: see field of fractions.)
We can also define a total order on Q by writing
The integers may be considered to be rational numbers by the embedding that maps  to
to ![[(p, 1)],\,](../../images/142/14268.png) where
where ![[(a,b)]\,](../../images/142/14269.png) denotes the equivalence class having
denotes the equivalence class having  as a member.
as a member.
Properties
The set  , together with the addition and multiplication operations shown above, forms a field, the field of fractions of the integers
, together with the addition and multiplication operations shown above, forms a field, the field of fractions of the integers 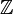 .
.
The rationals are the smallest field with characteristic zero: every other field of characteristic zero contains a copy of  . The rational numbers are therefore the prime field for characteristic zero.
. The rational numbers are therefore the prime field for characteristic zero.
The algebraic closure of  , i.e. the field of roots of rational polynomials, is the algebraic numbers.
, i.e. the field of roots of rational polynomials, is the algebraic numbers.
The set of all rational numbers is countable. Since the set of all real numbers is uncountable, we say that almost all real numbers are irrational, in the sense of Lebesgue measure, i.e. the set of rational numbers is a null set.
The rationals are a densely ordered set: between any two rationals, there sits another one, in fact infinitely many other ones. Any totally ordered set which is countable, dense (in the above sense), and has no least or greatest element is order isomorphic to the rational numbers.
Real numbers and topological properties of the rationals
The rationals are a dense subset of the real numbers: every real number has rational numbers arbitrarily close to it. A related property is that rational numbers are the only numbers with finite expansions as regular continued fractions.
By virtue of their order, the rationals carry an order topology. The rational numbers also carry a subspace topology. The rational numbers form a metric space by using the metric d(x, y) = | x − y |, and this yields a third topology on  . All three topologies coincide and turn the rationals into a topological field. The rational numbers are an important example of a space which is not locally compact. The rationals are characterized topologically as the unique countable metrizable space without isolated points. The space is also totally disconnected. The rational numbers do not form a complete metric space; the real numbers are the completion of
. All three topologies coincide and turn the rationals into a topological field. The rational numbers are an important example of a space which is not locally compact. The rationals are characterized topologically as the unique countable metrizable space without isolated points. The space is also totally disconnected. The rational numbers do not form a complete metric space; the real numbers are the completion of  .
.
p-adic numbers
In addition to the absolute value metric mentioned above, there are other metrics which turn  into a topological field:
into a topological field:
Let  be a prime number and for any non-zero integer
be a prime number and for any non-zero integer 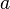 let
let 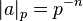 , where
, where  is the highest power of
is the highest power of  dividing
dividing 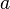 ;
;
In addition write  . For any rational number
. For any rational number 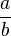 , we set
, we set 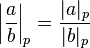 .
.
Then  defines a metric on
defines a metric on  .
.
The metric space  is not complete, and its completion is the p-adic number field
is not complete, and its completion is the p-adic number field  . Ostrowski's theorem states that any non-trivial absolute value on the rational numbers
. Ostrowski's theorem states that any non-trivial absolute value on the rational numbers  is equivalent to either the usual real absolute value or a p-adic absolute value.
is equivalent to either the usual real absolute value or a p-adic absolute value.